發布時間:2021-07-24所屬分類:經濟論文瀏覽:1次
摘 要: 摘要:概率統計對人們的實際生活有著十分重要的影響。概率與統計的方法日益滲透到各個領域,并廣泛應用于自然科學、經濟學、醫學、金融保險甚至人文科學中。為此,文章結合概率統計的基本內容,就其在經濟生活中的具體應用問題進行策略分析。 關鍵詞:概率統
摘要:概率統計對人們的實際生活有著十分重要的影響。概率與統計的方法日益滲透到各個領域,并廣泛應用于自然科學、經濟學、醫學、金融保險甚至人文科學中。為此,文章結合概率統計的基本內容,就其在經濟生活中的具體應用問題進行策略分析。
關鍵詞:概率統計;經濟生活;應用
概率統計是計算研究隨機現象統計規律的一門學科,是數學的一個重要分支。概率統計不僅具備獨特的理論思想方法,而且隨著現代社會科學技術的發展。概率論的基本應用方式是根據大量同類隨機現象的統計規律來對隨機現象中出現的某一種結果可能性進行客觀定義。為了能夠更好的讓人們認識到概率統計學習的必要性,文章著重就概率統計方法在社會經濟生活中的應用問題進行探究。
一、概率統計在風險決策中的應用
在一個概率統計預測系統中事物的狀態分為定型和不定型兩個狀態,某金融部門商業貸款的狀態可以簡單劃分為能夠收回的和不能夠收回的,如果處于能夠收回的狀態,下一個階段的狀態可能是貸款能收回狀態,也可能是貸款無法收回的狀態。但如果處于不能夠收回的狀態,下期狀態只能夠是貸款不能夠收回。在這樣的情況下可以發現能夠收回的狀態是一種不定型的狀態,不能夠收回的狀態是一種定型狀態。這兩個狀態在經過多次轉移之后形成各自的狀態轉移概率矩陣,使用定型狀態下的狀態轉移概率矩陣和金融機構的帶寬金額向量乘積能夠預測金融機構商業貸款中能夠回收和不能夠回收的金額是多少。
假設一個金融部門商業貸款按照時間的長短分為一年以內、一年到五年、五年以上三種。第一種貸款的20%可以收回,80%轉變為一年到五年貸款;一年到五年貸款有一半能夠收回,其他轉變為五年以上貸款;五年以上貸款有90%能夠收回,10%轉變為不能夠收回。這個貸款的額度分別為400萬、300萬、300萬。預測經過多次轉移之后一共的1000萬貸款中有多少可以收回?
相關知識推薦:統計分析學論文發表方法
在這個資料中將一年以內的貸款看作是狀態1,將一年到五年的貸款看作是狀態2,五年以上的貸款看作是狀態3。將五年以上能夠收回的貸款看作是狀態4,將五年以上不能收回的貸款看作是狀態5。應用馬爾科夫預測方式通過對定型狀態和不定型狀態的多次轉移分析,之后將其和三種貸款金額相乘,最終得到經過多次轉移之后一共的1000萬貸款中有61萬是不能夠收回的。
二、概率統計商品銷售中的應用
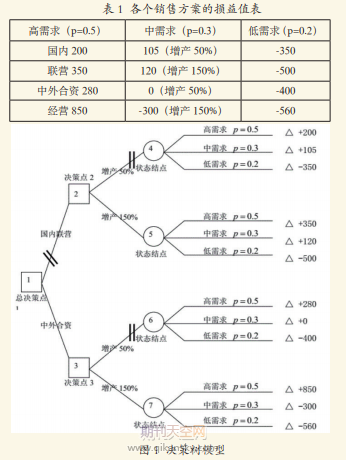
某電視廠在發展的過程中為了能夠增強自身的市場競爭力,制定了兩種經營方式,第一種是國內聯營,第二種是中外合資。在經過專業人員的估計分析之后總結出國內聯營和中外合資經營簽約成功可能性為100%,基于此制定出兩個生產方案,第一個生產方案是產量增加50%全部內銷,第二個生產方案是產量增加150%部分外銷,其他的都內銷。在進行市場調查研究和預測后制定出各個銷售方案的損益值表,如表1所示。文本內容是一個多級決策的問題,按照題目的意思繪制出如圖一所示的決策樹圖,根據決策圖內容優先計算第二季決策點的期望數值,即判斷增產50%方案適合還是增產150%的方案適合。決策樹模型如圖1所示。
三、概率統計在超市收款臺模擬選擇的應用
在生活中我們經常看到這樣一個現象:超市的門口平行排列多個收款臺,顧客帶著商品在收款臺之前排隊等待驗收貨物和進行付款。在平時,僅僅有幾個收款臺在工作,排隊人數十分穩定,在下班高峰期的時候排隊的隊伍增加,收款臺逐漸開放,排隊的人數開始回到開始的水平。這個現象從概率統計分析角度來看,超市排隊的人數不僅和收款臺的數量存在關系,而且也和顧客的多少、服務的速度存在關系,通過打造數學分析模型能夠更好地描述這些數量關系。顧客到達規律、服務時間和排隊的規劃都是存在隨機的,屬于一個隨機的服務類型。為了能夠解決這個問題,需要做出如下的假設:
(一)模型假設
1.泊松過程。假設顧客到達超市的過程中是泊松過程,假設N(t)代表的是時間間隔[0,t]內達到的來客人數(t>0),定義Pn在[t1,t2]中有n個到達的概率。如果滿足以下是哪個條件則是可以稱來客到達服從泊松過程。①任意兩個互相不重疊時間間隔內來客到達數量是相互獨立的。②在[t,t+△t]時間內來客達到數量僅僅和時間間隔長度有關,和起點時間不存在關聯。③在充分小的時間內間隔△t內,最多只有一個來客到達。結合上文條件分析,截止時刻t,有n個來客來訪的概率pn(t)=(λt)ne/n!t>0(n=0,1,2...K)。
2.排隊論。第一,輸入過程。來客來訪的過程具備以下的特點:來客的總體組成是無限的,來客到來的方式是一個接連一個的,來客相繼到來的間隔時間是隨機的,來客的到達相互獨立,輸入過程平穩,可以把顧客的到來考慮成是一個泊松過程。第二,排隊規則。來客到達的時候如果所有服務臺都被使用,排一個隊等候。第三,服務機構。服務機構有多個服務臺,彼此平行排列,服務時間隨機、分布平穩。
(二)模型的應用
來客期望數為:E(x)=ρρ1n/μnn!(1-ρ)2+ρ1=126服務時間期望為:E(t)=[ρ1nP0/n!(1-ρ)3(nμ)2]P0-[ρ12n/n!(1-ρ)3(nμ)2]+1/μ2=0.014
根據上文的假設分析發現超市在高峰期接待人數區間范圍為(96,156),服務時間區間為(1,1.24)D。
四、概率統計在保險問題中的應用
已知一個人壽保險公司有2500人參加保險,在一年時間內這些人的死亡概率為0.001,每人每年頭一天向保險公司交付的保險費用是12元,死亡時家屬可以從保險公司領取2000遠動保險金,求保險公司一年中獲利不少于10000元的概率和保險公司的虧本概率。
假設一年內死亡人數是X,死亡率p=0.001,將考慮2500人在一年內是否死亡看做是2500重Bernoulli試驗,則np=2500x0.001=2.5.np(1-p)=2500x0.001x0.0999=2.4975.保險公司每年收入為2500x12=30000,付出2000x元,根據中心極限定理得到保險公司一年中獲利不少于10000元的概率為p(30000-2000x≥10000)=p(0≤X≤2)=0.3174。保險公司的虧本概率為p(30000<2000x)=p(x>15)≈0。最終計算得到保險公司虧本概率趨近于0。
五、結語
綜上所述,概率論知識在人們的日常生活和企業管理、社會經濟運轉中發揮著十分重要的作用,通過合理利用概率統計理論知識能夠更好的促進社會經濟發展,提高企業發展效益,幫助人們掌握更多生活訣竅。——論文作者:武相宇
SCISSCIAHCI