發布時間:2022-02-16所屬分類:工程師職稱論文瀏覽:1次
摘 要: 摘 要:針對滾動軸承早期故障特征微弱,在強噪聲下難以識別的問題,提出了一種基于軟閾值歸一化奇異值占比(SNSR-SVD)為準則的奇異值分解重構的方法。這種方法能夠兼顧軸承早期故障特征的周期性和非平穩性,在重構信號中引入更多故障特征的細節信息。并且為了能夠更好的
摘 要:針對滾動軸承早期故障特征微弱,在強噪聲下難以識別的問題,提出了一種基于軟閾值歸一化奇異值占比(SNSR-SVD)為準則的奇異值分解重構的方法。這種方法能夠兼顧軸承早期故障特征的周期性和非平穩性,在重構信號中引入更多故障特征的細節信息。并且為了能夠更好的提取軸承的沖擊信號,將使用本方法重構后的信號通過以最大譜峭度法優化最優頻率與帶寬的濾波器,最后對濾波后的信號進行包絡解調分析。通過與其他方法進行仿真與實驗的對比驗證,證明本方法的優越性。
關鍵詞:奇異值分解;軟閾值;NSR;最大譜峭度;軸承
1 引言
滾動軸承是旋轉機械的關鍵部件,它的運行狀態直接影響旋轉機械的性能[1]。但是由于軸承的早期故障信號往往比較微弱,而且外界噪聲較大,干擾嚴重,因此常常被淹沒在干擾噪聲之中,難以識別。所以研究一種能夠抑制外界噪聲,較好提取軸承故障特征的檢測方法,不僅能夠提高旋轉機械使用壽命,更是保證其正常運行的關鍵。
奇異值分解(singular value decomposition 簡稱 SVD)作為一種零相位,零時間偏移的信號處理方法,在故障特征提取領域得到了廣泛的應用[2]。在使用 SVD 進行信號的降噪處理時,最大的難點在于奇異值的有效秩次難以確定[3]。 假如參與重構信號的奇異值過多,就會使重構信號混入一部分的噪聲,從而降低信號的信噪比,無法起到降噪的目的。而選擇過少,則會失去信號的有用成分,有時甚至會造成信號波形的畸變。奇異值能夠達到消噪處理的原理,是使用 Hankel 矩陣構造法構造軌跡矩陣時,周期信號組成的矩陣相鄰兩行具有高度相關性,進而產生奇異值的前幾項的值遠遠超過后面所有項的現象,我們稱之為周期信號的奇異值集聚性。而噪聲信號組成的相鄰兩行是完全不相關的,因此噪聲信號的所有項的奇異值是近似的。所以當采用奇異值前幾項進行重構時,就會使在重構信號中產生抑制噪聲的效果。基于此原理,眾多研究學者提出了確定奇異值有效秩次方法,均取得了一定的效果。其中趙學智等[4]提出使用奇異值差分譜法,選取奇異值差分譜最大峰值處作為奇異值重構的有效降噪階次,并將該方法應用在車床主軸箱故障診斷中,取得了良好的效果。楊文賢等[5]提出奇異熵增量法確定有效奇異值的秩次,降噪效果也比較好。胡林等[6]提出了奇異值增量曲率法確定奇異值的有效秩次,對于微弱信號的檢測,其檢出概率明顯上升。孟宗等[7]提出了奇異值累積法以確定奇異值的有效秩次,所獲得的提取信號的信噪比大幅度提升。但是,我們必須清楚的認識到,由于滾動體和保持架相對隨機滑動等現象無法避免[8],因此故障激發的沖擊將從原來的相同時間間隔變為波動間隔。所以滾動軸承真實的故障信號是一種非平穩的,非線性的信號[2]。而這種非平穩,非線性將導致在進行信號的奇異值分解時,故障特征的奇異值將不會集中在前幾項,而是向其他項分散。此時單單利用奇異值集聚性進行降噪處理,將顯得力不從心。
基 于 上 述 分 析 , 本 文 提 出 以 歸 一 化 奇 異 值 占 比(normalized singular value ratio 簡稱 NSR)為重構準則的奇異值分解法,此方法兼顧考慮周期分量奇異值積聚性和非線性,非平穩信號向其他項分散的性質的特性,能夠較好的處理滾動軸承早期微弱故障的特征提取。當使用歸一化奇異值占比的方法進行重構的信號,會引入較多的噪聲,為增大前面分量所占比重,并節約計算時間,本文提出適合奇異值分解的軟閾值函數(soft threshold function)作為其加權和截至條件,以提高重構信號的信噪比。最后為了更好的提取軸承信號中的沖擊特征,結合前人方法[10],在重構信號之后,以最大譜峭度為準則選取濾波器合適的中心頻率以及帶寬進行濾波,并使用包絡譜進行分析,經過仿真信號與實驗數據的對比分析,證明本文方法所提取的特征信號更加真實,取得了良好的效果。
2 算法簡介
2.1 奇異值分解(SVD)
2.2 歸一化奇異值占比重構法(NSR)
為了能夠充分利用 SVD 分解后各分量信息,避免在非線性,非平穩條件下僅采用前幾項奇異值較大的分量進行信號重構,導致微弱故障特征被剔除或難以反映內在規律的現象,提出了一種基于(normalized singular value ratio)NSR 的奇異值分解重構法進行重構,使更多的奇異值分量都參與信號重構,兼顧了微弱故障的信息。
3 軟閾值 SNSR-SVD 故障特征提取流程
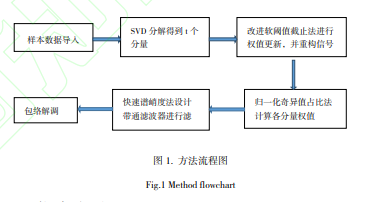
根據上面的理論分析,本文擬提出基于 SNSR-SVD 的故障特征提取方法,首先將故障信號進行奇異值分解,使用式(4)計算各奇異值的占比,并進行歸一化處理,計算其歸一化占比值。隨后將計算的歸一化占比的各分量權重值引入式(7)得到基于軟閾值的奇異值占比的各分量信號的權重。并進行信號重構。將重構后的信號計算最大譜峭度所在的頻率,并將重構信號通過以此頻率作為共振解調最優中心頻率和帶寬的帶通濾波器,最后對通過濾波器的信號進行包絡分析。其具體流程如圖 1 所示。
利用奇異值差分譜和奇異熵增量曲率譜兩種方法對仿真信號進行降噪處理,由圖 3 可知,奇異值差分譜確定的有效秩次為 5,奇異熵增量曲率譜的有效秩次為 15,采用上述兩種方法確定的有效秩次對信號進行 SVD 重構,獲得的時域波形和頻域波形如圖所示。
由圖 4 所示,采用奇異值差分譜和奇異熵增量曲率譜對信噪比較低的仿真信號進行降噪處理的效果并不理想,無法辨別故障信號的頻率特征,信號特征發生了畸變。當采用本文方法對仿真信號降噪處理的譜峭度以及包絡譜如圖 5 a, b 所示。
根據文獻[9]的方法進行快速譜峭度分析,以確定最優頻率和帶寬,快速譜峭度是一個彩色圖,其顏色代表不同頻率下的峭度的大小,顏色越明亮,譜峭度值越大。使用本文方法進行最大譜峭度優化時的峭度值為 2.9,此時的頻域波形圖為圖5(b),有圖5(b)可以較為清楚的分析出仿真信號的倍頻成分,分析故障信號的故障特征。
5 實驗驗證為驗證
本文方法的有效性,選用美國凱斯西儲大學(Case Western Reserve University)軸承數據中心的數據進行驗證[11]。信號取自實驗系統的驅動端的振動信號,采樣頻率為 12000Hz。試驗采用電火花加工技術在滾動軸承上布置單點損傷。軸承的型號是 6205-2RS JEM SKF,為深溝球軸承,軸承的滾動體個數 n=9,內圈直徑為 25mm,外圈直徑為 52mm,厚度為 15mm,滾動體直徑為 7.94mm,節徑為 39.04mm。根據軸承故障特征頻率計算公式,計算當電機轉速為 1797r/min 時,軸承的外圈,內圈和滾動體的特征頻率如表 2 所示。
5.1 軸承內圈故障特征提取
用軸承內圈數據進行時域和頻域分析,如圖 6 所示。
為進一步對比本文方法,采用文獻[12]的方法進行對比分析,分別得到的包絡譜如圖 7a, b 所示。
由圖 7a,b 可以看出,在圖 a 中,故障信號的 2 倍頻和 3 倍頻處幅值基本相同,且雜波較多。在圖 b 中可以明顯看到倍頻的衰減現象,這表明更多的故障特征的細節信息得以呈現,且雜波的幅值也被抑制,證明了本文方法的有效性。
5.2 軸承外圈圈故障提取
用軸承外圈圈數據進行時域和頻域分析,如圖 8 所示。
由圖 9 a, b 可以看出,在圖像 a 上,外圈軸承信號雜波較多,在圖 b 中雜波的幅值抑制非常明顯,證明了本文方法的有效性。
6 結論
1.對比證明了在高噪聲背景下的軸承故障信號非線性將導致軸承故障特征的 SVD 分解奇異值發生了向相近奇異值移動的現象,此時僅采用前幾項分量進行信號重構,很容易丟失信號的特征,并導致信號發生畸變。
2.仿真證明了采用軟閾值歸一化奇異值占比法作為奇異值有效階次選擇方法,能夠更多的引入軸承故障特征的細節信息,對于提取軸承的早期故障特征有效。
3.實驗證明了使用 SNDR-SVD 作為有效秩次選擇方法,使用最大譜峭度作為構造濾波器帶寬和最優頻率的優化選擇法,能夠更好的識別沖擊信息,提取的故障特征更加真實有效。——論文作者:張震 1、2,劉保國 2,周萬春 1 , 劉時言 1
參考文獻:
[1] 欒孝馳,沙云東.降速工況下滾動軸承微弱故障特征信號提取新方法[J]. 機械設計與制造,2020(3):207-210. LUAN Xiaochi,SHA Yundong. A New Method of Rolling Bearing Weak Fault Characteristic Signal Extraction Under Lowing Speed Condition 【J】.Machinery Design &Manufacture, 2020(3):207-210.
[2] 黃晨光,林建輝,丁建明, 劉澤潮.一種新的差分奇異值比譜及其在輪對軸承故障診斷中的應用[J].振動與沖擊,2020,39(4):17-26. HUANG Chenguang,LIN Jianhui,DING Jianming, et al. A novel energy difference singular value ratio spectrum and its application to wheelset bearing fault diagnosis[J]Journal of Vibration and Shock , 2020,39(4):17-26.
[3] Ahmed S M , Al-Zoubi Q , Abo-Zahhad M . A hybrid ECG compression algorithm based on singular value decomposition and discrete wavelet transform[J]. Journal of Medical Engineering & Technology, 2007, 31(1):54-61.
[4] 趙學智,葉邦彥,陳統堅.奇異值差分譜理論及其在車床主軸箱故障診斷中的應用[J].機械工程學報,2010,46(1):100-108. ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Difference Spectrum Theory of Singular Value and Its Application to the Fault Diagnosis of Head stock Of Lathe [J].Journal of Mechanical Engineering, 2010,46(1):100-108
[5] Yang W X , Tse P W . Development of an advanced noise reduction method for vibration analysis based on singular value decomposition[J]. Ndt & E International, 2003, 36(6):419-432.
SCISSCIAHCI