發布時間:2021-12-31所屬分類:電工職稱論文瀏覽:1次
摘 要: 摘 要 在串行生產線中, 機器會發生隨機故障(即機器不可靠), 因此需要維修工人及時維修, 使得故障的機器恢復加工能力, 否則就可能導致系統吞吐率降低. 如何在滿足系統吞吐率的前提下, 使用盡可能少的維修工人來完成機器的維修任務, 本文稱這樣一個全新的問題為串行生產
摘 要 在串行生產線中, 機器會發生隨機故障(即機器不可靠), 因此需要維修工人及時維修, 使得故障的機器恢復加工能力, 否則就可能導致系統吞吐率降低. 如何在滿足系統吞吐率的前提下, 使用盡可能少的維修工人來完成機器的維修任務, 本文稱這樣一個全新的問題為串行生產線中機器維修工人的任務分配問題. 針對該問題, 本文首先建立了問題的優化模型, 并將該優化問題轉換為多個判定問題進行求解; 然后, 通過合理地定義機器的維修工作量, 使得判定問題可以類比為并行機調度問題; 最后, 采用了一種基于最長處理時間優先算法(Longest Processing Time, LPT)和回溯策略的啟發式算法, 搜索最優的維修工人任務分配方式. 實驗結果表明, 該方法能有效求解維修工人的任務分配問題.
關鍵詞 生產系統, 機器維修, 任務分配, LPT算法, 回溯策略
對于制造業來說, 其產品主要來自于龐大的生產線系統, 生產線的效率(吞吐率)越高, 企業效益往往也就越好. 然而生產線中的機器會發生隨機故障, 當生產線中某一臺機器發生故障時, 如果該機器沒有得到及時的維修, 就有可能使得系統吞吐率下降, 進而導致企業利潤減少. 本文假設一臺機器故障時, 只能由已分配的某一名維修工人進行維修, 顯然如果為每臺機器都配備一名維修工人, 那么所有的機器故障都會得到立即維修, 企業的損失也就最小. 然而, 這樣會導致維修工人在大多數時間都處于空閑狀態, 極大地增加了企業的用人成本. 如何在保證串行生產線系統吞吐率的情況下, 使用盡可能少的維修工人來完成機器的維修任務, 本文稱這樣一個問題為串行生產線中機器維修工人的任務分配問題.
在生產線領域, 已經存在有大量的資料, 文獻中主要通過排隊論[1]、分解[2]、仿真和近似[3−4]等方法來對生產線進行研究. 當前生產線領域的研究方向主要是生產線的性能分析和優化, 例如生產線平衡問題[5−6]和生產線中緩沖區大小分配問題[7−8]等. 然而, 盡管在生產線這一領域已經有了很多研究工作,但是根據文獻調研, 目前還沒有相關文獻在研究串行生產線中機器維修工人的任務分配問題. 這也就是說, 本文所研究的問題是一個全新的問題. 對于這樣一個新問題, 有三類問題與之具有一定相似性. 第一類問題是任務分配問題[9] , 該問題要求定義每一個任務分配給任意一個人的“成本”, 然而在本文所研究的問題中吞吐率是一個整體的性能指標, 難以定義每一個機器的維修任務分配給任意一個工人的“成本”, 所以不能應用分配問題的算法來求解本文的問題.第二類問題是裝箱問題[10−11] , 該問題要求將一定數量的物品放入容量相同的一些箱子中, 使得所用的箱子數目最少, 然而由于無法定義維修工人的“容量”(單個工人可以負責維修的機器數量), 所以也不能直接應用裝箱問題的算法來求解本文的問題. 第三類問題是并行機調度問題和文獻[12]中提出的線邊緩沖區分配問題(Line-side Buffer Assignment Problem, LBAP), 其中并行機調度問題要求使用一定數量的機器完成一些相互獨立的任務, 使得完成時間最短, 而LBAP問題則是要求在保證總裝線吞吐率的條件下, 使用給定數量的司機完成物料傳送任務. 由于第三類問題中的LBAP問題與本文所研究的新問題非常類似, 因此可以借鑒文獻[12]中提出的帶回溯的序貫分配算法(Sequential Assignment with Backtracking, SAB), 來求解本文所研究的問題. 該算法基于并行機調度問題[13]中的最長處理時間優先(Longest Processing Time, LPT)算法[14−15]和回溯策略, 是一種啟發式算法.
本文的貢獻在于: 第一, 本文提出了一個全新的問題——串行生產線中機器維修工人的任務分配問題, 并對其進行了建模; 第二, 合理地定義了機器的維修工作量, 使得本文所研究的問題可以類比為并行機調度問題; 第三, 通過仿真實驗, 驗證了文獻[12]中提出的SAB算法, 對本文所研究的問題同樣適用, 該方法在保證系統吞吐率的前提下, 能夠有效減少企業的用人成本.
本文的結構安排如下: 第一節介紹串行生產線, 建立問題模型和仿真模型; 第二節定義和量化機器以及工人的維修工作量, 并對維修工人數量的下界進行估計; 第三節描述帶回溯的維修工人任務分配算法; 第四節進行仿真實驗, 驗證本文方法的有效性; 最后對本文的內容和貢獻進行總結.
1 系統模型
1.1 串行生產線模型
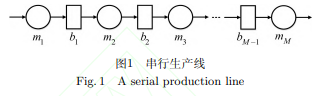
串行生產線是指: 將機器以串行方式連接起來, 并通過物料儲運設備將工件從第一個機器輸送到與它相鄰的下一個機器的生產系統, 如圖1所示, 其中圓圈表示機器, 方框表示物料儲運設備(即緩沖區). 在實際生產過程中, 機器總是會發生隨機故障(即機器不可靠), 這些故障造成的影響會沿著生產線向上游和下游的機器傳播. 例如, 當圖1中的機器m2發生故障時, 其下游的機器m3不久便會加工完緩沖區b2中的所有工件, 然后進入饑餓狀態, 同時機器m1則會在充滿緩沖區b1后進入阻塞狀態. 如果此時機器m2仍然沒有被修復, 那么饑餓狀態會繼續向下游傳播直至最后一臺機器mM. 類似的, 阻塞狀態也會向上游傳播, 這種饑餓或堵塞的情況越嚴重, 串行生產線的吞吐率也就越低.
1.2 問題模型
圖2給出了一個串行生產線中維修工人任務分配的例子, 其中實線部分表示一個擁有4臺機器的串行生產線系統, 虛線部分表示一個擁有2名機器維修工人的維修排隊系統. 當生產線中的某一臺機器發生故障后, 該機器就會停止加工, 并進入到維修排隊系統, 維修完成之后, 再返回生產線系統. 在圖2中, 機器m1和機器m2的維修任務分給了維修工人r1, 而機器m3和機器m4的維修任務則分給了維修工人r2. 顯然, 當改變維修工人的數量以及機器維修任務的分配方式時, 維修效率都可能會受到影響, 從而導致生產線的吞吐率發生變化. 那么如何合理分配機器的維修任務, 使得能夠用盡可能少的維修工人, 滿足串行生產線的吞吐率要求, 就成為了本文研究的核心內容.
3 帶回溯的維修工人任務分配算法
由于本文所研究的判定問題(P2)與文獻[12]中所研究的LBAP問題是同一類問題, 所以在求解判定問題(P2)時, 可以借鑒文獻[12]中提出的SAB算法. 同時, 因為LBAP問題與并行機調度問題具有一定相似性, 所以SAB算法結合了并行機調度問題的經典解法, 即LPT算法(一種貪心算法), 并在此基礎上引入了回溯策略, 使得該算法能夠快速求得可行解, 并且以概率1收斂. 另外, 文獻[12]中還將SAB算法與遺傳算法進行了對比, 證明了在解決LBAP問題時, SAB算法的優越性. 在解決本文所研究的問題時, 采用LPT算法是因為判定問題(P2)與并行機調度問題也具有很強的相似性, 這一點在2.1節中已經進行了說明. 在并行機調度問題中要使任務總完成時間盡可能減少, 則需要使各個機器的任務量盡可能平均. 那么同理, 在判定問題(P2)中, 要提高生產線吞吐率, 則需要平衡維修工人的忙閑程度, 該步驟通過LPT算法即可實現. 而引入回溯策略則有兩個原因: 首先, 由于串行生產線的吞吐率是由仿真得到的, 而仿真是帶有一定誤差的, 并不能完全代表真實值; 其次, 一般來說維修工人的忙閑程度越平衡, 系統吞吐率越高, 但是由于串行生產線系統的復雜性和隨機性, 導致維修工人的忙閑程度最平衡時, 并不表示系統吞吐率也一定最高, 所以需要回溯來尋找更優的可行解.
參考SAB算法, 本文約定如果在一個分配方案中, 所有的機器都被分配給了維修工人, 則稱這樣的一個分配為完全分配, 否則稱之為部分分配. 對于一個部分分配A來說, 如果在此基礎上, 再分配一臺機器, 得到部分分配或者完全分配A0 , 則稱A為A0的父分配, 稱A0為A的子分配. 假設未分配的機器都不會發生故障, 那么顯然, 當一個部分分配的系統吞吐率小于T P0, 該部分分配的子分配也都不滿足吞吐率要求. 通過這一性質, 我們便可以在算法的步驟5)中, 引入回溯策略, 確定下一步的搜索方向.
算法的具體步驟如下:
1)初始化N = Nlean, 并設置一個小的正數², 且0 < ² < 0.5, ²的值會影響回溯概率Pb, 同時設回溯次數為nb, nb的大小將影響單個判定問題中回溯尋找可行解的次數.
2)按照LPT算法的思想進行貪心分配, 將機器維修工作量Wr j 從大到小排序, 逐個將未分配的機器中Wr j 最大的機器, 分配給當前任務量最小的維修工人, 記當前分配方式為A.
3)仿真得到當前分配方式的吞吐率T P(A). 如果T P(A) < T P0, 則將N加1, 并返回步驟2), 否則說明直接通過貪心分配已找到一個可行解, 可以開始回溯尋找更優的可行解.
4)將N的值減1, 按照步驟2)中貪心分配的方法重新分配任務, 并更新當前分配方案A, 進入步驟5).
5)仿真得到當前分配方案A的吞吐率T P(A), 若T P(A) < T P0, 則設置回溯概率Pb = 1 − ², 否則設Pb = ². 產生一個滿足(0,1)均勻分布的隨機數ζ, 當A為一個部分分配時, 如果存在i ∈ {1, 2, . . . , N}, 使得子分配的生產線系統吞吐率滿足要求, 并且有(i − 1) · (1 − Pb)/N < ζ ≤ i · (1 − Pb)/N, 則用該子分配替換當前分配, 否則使用A的父分配替換當前分配; 當A是一個完全分配時, 如果ζ ≤ 1 − Pb并且T P(A) ≥ T P0, 則保持A為當前分配, 并記錄當前分配為一個可行解, 否則使用A的父分配取代當前分配. 將nb減1, 如果nb = 0, 則進入步驟6), 否則返回步驟5).
6)若在步驟5)中找到可行解, 則返回步驟4)尋找更優的可行解, 否則算法結束.
算法說明: 步驟1)-3), 通過簡單的貪心分配, 可迅速獲得一個可行解, 縮小搜索范圍; 步驟4)-6)結合貪心分配和回溯策略, 求解優化問題(P1), 其實質是對于多個判定問題(P2)的求解. 在步驟4)-6)中對于單個判定問題求解時, 本文的算法與文獻[12]中的SAB算法基本相同, 其不同點僅在于本文的算法步驟中, 去除了SAB算法里可行解的可信度這一參數. 這是由于本文在求解吞吐率時, 仿真時間設定較長, 吞吐率的精度已經可以滿足實驗要求, 為了簡化算法步驟, 則去除了該參數.
4 實驗結果及分析
為了驗證本文方法的有效性, 4.1節將對一條具有8臺機器的串行生產線進行仿真實驗, 并對仿真結果進行定性分析. 4.2節將仿真一條具有50臺機器的串行生產線, 其中機器的參數帶有一定隨機性, 由此進一步來驗證本文方法的可靠性.
4.1 8臺機器串行生產線仿真實驗
本節采用一條具有8臺機器的串行生產線, 設定所有機器的可靠性模型為指數可靠性模型, 機器之間的緩沖區容量均設為5個工件, 機器的加工節拍統一設置為1(分鐘), ²取值為0.15, 機器的其他具體參數如表1所示.
對于這樣一條具有8臺機器的串行生產線, 本節首先對其分配8個維修工人, 使得所有的維修任務都能及時得到維修, 通過仿真得到系統的最大吞吐率T Pmax = 0.8868. 由于當維修工人數量小于機器數量時, 其吞吐率必然小于等于為每一臺機器都分配一個維修工人時生產線系統的吞吐率, 所以可以設定T P0 = 0.95 ∗ T Pmax = 0.8424, 當仿真求出的系統吞吐率大于等于T P0時, 即認為該分配方式滿足系統要求. 實驗所得到的系統吞吐率和工人數量如表2所示, 同時表3中給出了具體的維修工人任務分配方案.
由表2可知, 當回溯次數為0時, 即就是只采用簡單的貪心分配進行求解時, 得出所需的維修工人數量為5. 當設置回溯次數為10, 則得到了只需要4個維修工人的分配方案, 當回溯次數增加到50后, 找到了維修工人數量為4時, 吞吐率更大的可行解. 實驗結果表明: 對于機器參數給定的小型串行生產線, 本文的方法能夠快速的求解出一個比較好的解, 同時隨著回溯次數的增加, 找到更優的可行解的可能性也隨之增加.
4.2 50臺機器串行生產線仿真實驗
在4.1節中, 為了方便分析, 采用了一條相對簡單的具有8臺機器的串行生產線, 其中機器的維修率、故障率以及加工周期都是直接給定的. 本節將采用一條具有50臺機器的串行生產線進行仿真實驗, 仍舊設定所有機器的可靠性模型為指數可靠性模型, 機器之間的緩沖區容量為5個工件, ²取值為0.15. 但是, 機器參數的設置更為隨機, 令50臺機器的故障率λ、維修率µ和加工節拍τ分別為滿足(0,1)、(2,10)和(0.8,1.2)的均勻分布.
對于這樣一條具有50臺機器的串行生產線, 首先對其分配50個維修工人, 仿真得到T Pmax = 0.6930, 設定T P0 = 0.95 ∗ T Pmax = 0.6584, 然后按照算法步驟進行求解, 實驗結果如表4所示.
由表4可知, 當只采用貪心分配時, 得到所需的工人數量為17, 當設置回溯次數為100時, 得到了只需要15個維修工人的分配方案, 節省了2個維修工人. 實驗結果表明: 當串行生產線的機器參數為帶有隨機性的值時, 本文的方法仍然能夠獲得較好的可行解; 另外, 隨著機器數量的增加, 解空間的規模呈爆炸性增長, 此時通過本文算法中的貪心分配仍可以迅速得到一個可行解, 同時通過回溯機制通常也可以找到更優的可行解.
5 結論
本文研究了串行生產線中機器維修工人的任務分配問題, 給出了一套系統化的解決方案. 首先, 本文構建了所研究問題的優化模型, 并將其轉換為多個判定問題進行求解, 同時建立了串行生產線的仿真模型來求解系統吞吐率; 然后, 合理地定義了機器的維修工作量, 使得判定問題可以類比為并行機調度問題, 并估計了維修工人數量的下界; 最后, 采用一種基于LPT算法和回溯策略的啟發式算法, 對該問題進行了求解. 實驗結果表明, 本文采用的方法在不同機器數量和不同機器參數的串行生產線中, 都能較好的解決維修工人的任務分配問題, 在保證系統吞吐率的前提下, 有效地減少了企業的用人成本.——論文作者:鄢超波1, 2 張雷1, 2
SCISSCIAHCI