�l(f��)���r�g��2018-01-25���ٷ������Փ���g�[��1��
ժ Ҫ�� ����Ϣ���g(sh��)��(y��ng)�õ����Д�(sh��)�W(xu��)�ν̌W(xu��)�У����Ժ��n�ý̌W(xu��)�M���ЙC�ĽY(ji��)�ϣ���(sh��)�W(xu��)�n�ó�M����͘�Ȥ�������ˏ�(f��)�s�����֪�R����(sh��)�W(xu��)�n�ÿ��Գɞ�W(xu��)���W(xu��)��(x��)�Ę��@������������Ҫ��B�ή����ڳ��Ўν̌W(xu��)�еđ�(y��ng)�ã��挦���n�ý̌W(xu��)��׃�������F(xi��n)�n�ý̌W(xu��)�F(xi��n)����
��������Ϣ���g(sh��)��(y��ng)�õ�������(sh��)�W(xu��)�ν̌W(xu��)�У����Ժ��n�ý̌W(xu��)�M���ЙC�ĽY(ji��)�ϣ���(sh��)�W(xu��)�n�ó�M����͘�Ȥ�������ˏ�(f��)�s�����֪�R����(sh��)�W(xu��)�n�ÿ��Գɞ�W(xu��)���W(xu��)��(x��)�Ę��@������������Ҫ��B�ή����ڳ��Ўν̌W(xu��)�еđ�(y��ng)�ã��挦���n�ý̌W(xu��)��׃�������F(xi��n)�n�ý̌W(xu��)�F(xi��n)������ͨ�^��Ϣ���g(sh��)�̎����õ�����(d��o)�W(xu��)��ͨ�^֪�R�ČW(xu��)��(x��)���˽����֪�R�ı��|(zh��)���w�����c�W(xu��)�^���е�˼�S��
�������P(gu��n)�I�~���ӑB(t��i)�о���,��Ϣ���g(sh��)�̌W(xu��),��(sh��)�W(xu��)�̌W(xu��)�ı��|(zh��),�ή����o���̌W(xu��)
������Ϣ���g(sh��)�c���Д�(sh��)�W(xu��)�̌W(xu��)���ںϣ��������ìF(xi��n)����Ϣ���g(sh��)�ă�(y��u)�����c������̎��Ľ̌W(xu��)�o�����ߡ���м���ߺ͌W(xu��)�����J(r��n)֪���ߣ����D�Ρ���(sh��)�֡��Ӯ��������������Ƚ̌W(xu��)��Ҫ�M�оC��̎����ʹ�ÌW(xu��)��������������գ����õ����B(y��ng)�W(xu��)���Ą�(chu��ng)�����R����(chu��ng)�¾���(chu��ng)�������ͽ�Q���H���}����������(sh��)�W(xu��)֪�R�����dz���Ҫ������(sh��)�W(xu��)֪�R�����d��˼�S��������Ҫ���҂���(y��ng)ԓ�W(xu��)���ă�(n��i)��ϲ�g˼�����W(xu��)��˼���������҂��̎����n�̵�˼�S���c�����w��֪�R�}�j(lu��)���Y(ji��)��(g��u)Ҫ���Լ���˼�������⣬Ȼ�����n���Ͻ̽o�W(xu��)��һ�N˼�����о���(sh��)�W(xu��)���}�ķ�����
�����ή����o���̌W(xu��)�M����Д�(sh��)�W(xu��)���n�ã���ʹ����ĸ�����w�����������������M�ЄӑB(t��i)����ʾ�����a�˂��y(t��ng)�̌W(xu��)��ʽ��ֱ�^�С����w�к̈́ӑB(t��i)�еȷ���IJ��㡣�����@�����c��̎�������̌W(xu��)�ֶ��y��̎���Ć��}�����������W(xu��)�����dȤ������������ֱ�^ӡ�ή����̎�����̌W(xu��)�y�c��ͻ�ƽ̌W(xu��)���c������n��Ч�ʺͽ̌W(xu��)Ч���ṩ��һ�N�F(xi��n)�����Ľ̌W(xu��)�ֶΡ�
��������(x��)�}�n����(f��)��(x��)�n���҂��̎���(j��ng)�����������n�͡��҂����ӱ�������������(x��)�}�n����ͨ�^��(x��)�}�̌W(xu��)����(d��o)�W(xu��)�����┵(sh��)�W(xu��)֪�R�ı��|(zh��)���γ�˼�S������?ͨ�^��(sh��)�W(xu��)�W(xu��)��(x��)���H�õ�һЩ������(sh��)�W(xu��)֪�R�ͷ���������Ҫ�������B(y��ng)һ�N˼�S��ʽ��һ�N���\�����е�֪�R��Q���}�����������B(y��ng)�����@��˼�S��(x��)�T���ˣ��@���ǔ�(sh��)�W(xu��)�W(xu��)��(x��)�ı��|(zh��)��
�����P����һ���п����}�������c�������ή���ͨ�^�������Ξ鱳���ĎΈD�εķ�����������D���P(gu��n)ϵ�����ö�N�������F(xi��n)����Ⱦ��μ���λ���P(gu��n)ϵ���C�������B(y��ng)�W(xu��)����Ƕ�˼�����}��˼�S��(x��)�T��ͨ�^���cP��߅BC����ֱ�����Ƅӣ��W(xu��)���M�в��롢Փ�C�����\�ӵĽǶ��ٴ����↖�}�ı��|(zh��)���M�����������D(zhu��n)�������Σ�̽���Y(ji��)Փ�����ėl�����ڈD��׃�����^���У�ͨ�^ȷ�ʽ���Mһ�����↖�}�γɵ�ԭ���w�����������c���[�����ڎΆ��}�о��^���е���Ҫ���x��
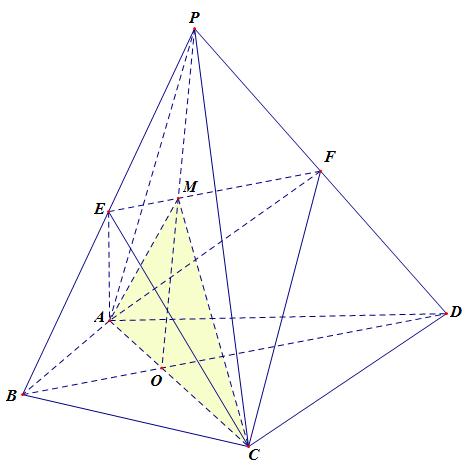
�������}1����D1����������ABCD�У�BD��һ�l���Ǿ����cP��߅BC��(�c�cC��B���غ�)���B��AP��ƽ�ơ�ABP��ʹ�cB�Ƅӵ��cC���õ���DCQ���^�cQ��QH⊥BD��H���B��AH��PH�� ̽����AH�cPH�Ĕ�(sh��)���P(gu��n)ϵ�cλ���P(gu��n)ϵ�������C����
����չʾ��N���������B(y��ng)�l(f��)ɢ˼�S����
�����@���}Ŀ�кܶ�N�C����������������(d��o)�W(xu��)����Ƕȵ��J(r��n)�R�D���Լ��D���P(gu��n)ϵ������(ji��)�n�����ή����o���̌W(xu��)��һ������Ԍ�ȫ�ȵ��������M����䣬���õ،��җl��;��һ�������Îή���ĄӮ���ʾ�M�з��ۻ����D(zhu��n)�ȈD��׃�����D�΄��������w�D�����N���ă�(n��i)�ڵ��P(gu��n)ϵ��
�����}Ŀ�l�������@��һ���l����“��������ABCD�У�BD��һ�l���Ǿ�”��ͬ�r�[����BD��һ�l��ƽ�־��ėl������ô�҂����Խ�����ƽ�־��M���S���Q׃�Q��(g��u)��ȫ�������Ρ��҂����Կ��]��(g��u)���c��BPHȫ�ȵ���������D2�����������ε��S���Q�ԣ�����BHQ��BD���ۣ��õ���BHE���҂�ֻ���C����AHE�ա�PHB����;������EH⊥BH���������C��AH⊥PH��
����Ҫ�C��AH=PH����AH⊥PH�������҂�����ֱ���C����AHP�ǵ���ֱ�������Σ���ˣ��҂����Կ��]��AH��PH�������ֱ��������б߅�ϵ��о����C�����˷N�뷨���������ɷN�����팍�F(xi��n)����D3���^�cQ��BQ�Ĵ�����AH�����L����M���B��PM��Ҳ���ԏĽY(ji��)Փ���l(f��)����������ֱ�������ε����P(gu��n)֪�R�M�з��������Îή��������ε����L��(�ӑB(t��i)��ʾ���L�����γ��^��)���Լ��^���c����ֱ֪���Ĵ����Ĺ��ܣ���(g��u)������Ҫ��ȫ�������Σ���D4�����C����ֱ�ĕr��߀���Խ������c���A��֪�R�����Îή������A���@ʾ�[�ذ��o����D5���Ķ�ʹ���}�͈D���P(gu��n)ϵ���������ˡ�
�������ϵ�����(d��o)�����ή���ӑB(t��i)����ʾ���M�з��ۡ����D(zhu��n)�ȹ��ܣ�����(d��o)�W(xu��)�����õķ���������D���P(gu��n)ϵ���J(r��n)�R�D�ε������^�̣������W(xu��)�����õ��J(r��n)�R�D�Ρ�
��������ͨ�^��(g��u)�첻ͬ��ȫ�������Σ����B(y��ng)�W(xu��)���ij���˼�S��������(g��u)��ȫ����������Ҫ���D���J(r��n)�����������ھ�D����Ϣ�����ܘ�(g��u)����ܵ�ȫ�������Σ�����ԭ�D��ȱʧijЩȫ�������ε�Ԫ�أ���Ҫ�M�ЈD��߀ԭ���������ή����܉�ӑB(t��i)��ʾ߀ԭ���^�̣��ڴ��^�������B(y��ng)�W(xu��)���Ŀ��g�^��M�г���˼�S���������B(y��ng)��ͨ�^���D���P(gu��n)ϵ�ķ���������(d��o)�W(xu��)����ǶȵČ��}Ŀ����C�����Ķ��Mһ�����J(r��n)�R�ˈD���P(gu��n)ϵ��
������Q���c���}���M������̽��
�������Îή����еĄӮ����ܿ������ӡ��B�m(x��)�ر��F(xi��n)�\��Ч����������讋���\�ӌ�����\��܉�E������܉�E�������DŽӑB(t��i)�ġ��ģ���ֱ��F(xi��n)��܉�E�a(ch��n)����ȫ�^�̣��W(xu��)�����^�졢���y����C�������c�����Ȕ�(sh��)�W(xu��)����У��γ��Լ�����(sh��)�W(xu��)֪�R�����⣬�@�͞�W(xu��)���e�O���ӽ���(g��u)֪�R�wϵ�ṩ�ˌW(xu��)��(x��)��ƽ�_�����⣬�W(xu��)���о��ΈD�Εr��(j��ng)�����Ï�����D���ƏV��һ��D�εķ������ڎή����У�ֻҪ��һЩ���o�̈́Ӯ������磬�҂����cP�τ��˻ص��cB�����@�N����λ���P(gu��n)ϵ�¸����ڰl(f��)�F(xi��n)�Y(ji��)Փ��Ҳ���Ԍ��cP�τӵ�BC�����L���ϣ����ߌ��cP�τӵ�CB�����L���������M�ЈD��׃ʽ���B�����һ����о������������ή���ĄӑB(t��i)��ʾ����������n�Ì�Ч�ԣ�ͬ�r��ֱ�^�Ŀ����D�����N���ı��|(zh��)������
�����S�r��׃�}�O(sh��)�l�����M��׃ʽ�̌W(xu��)
�������Îή����M����(x��)�}�n�̌W(xu��)�r��Ҫ�M�����������S�r��׃�}�O(sh��)�ėl�����M��׃ʽ�̌W(xu��)���ṩ��N���ζ�N�ⷨ���ԝM��W(xu��)����֪�R�Ŀ������Ҫ�����^���ԣ���PPT��Flash�������n���ͺ��y�����@һ�c�����ή���Ϳ����p�ɸ㶨��
������(d��ng)�W(xu��)�����cP�������ε�߅BC��(�c�cC��B���غ�)�����������������҂�����������(d��o)�W(xu��)�������}�M����չ˼��������cP��ֱ��BC����?��(d��ng)������׃?y��u)����Ρ����Ρ�ƽ����߅���?�֕������ӵĽY(ji��)Փ��?���������������Ρ����ο����ГQ�İ��o���M�ЄӑB(t��i)��ʾ���l(f��)�F(xi��n)�D���P(gu��n)ϵ��
�������}2�� �������ΓQ�����Εr���^�cQ��QH⊥BD��H���B��AH��PH��AH=PH�@���Y(ji��)Փ��Ȼ������?Ո���D�f����
������(d��ng)������׃?y��u)�������Ȼ�M���}Ŀ�l���r��ͬ�W(xu��)�����l(f��)�F(xi��n)AH=PH�@���Y(ji��)Փ�������ˡ�
�����o�����o�W(xu��)�����˼����Ҫʹ�Y(ji��)Փ��������ô∠QHB��(y��ng)ԓ��Ҫ�M��ʲô�l����?
�����@�����}���ڌW(xu��)�����f��һ���y�ȣ����ǽ����ή���ӑB(t��i)��ʾ�����\�ӵ��^��������(d��o)�W(xu��)���l(f��)�F(xi��n)�Y(ji��)Փ�����ėl�����W(xu��)�������}���J(r��n)�R��ֱ�^�������̎��ڽ̌W(xu��)�r�������Îή����S�r׃�Q�D�ε��\�Ӡ�B(t��i)����(chu��ng)�������ڌW(xu��)���IJ��롢��C���C���ĭh(hu��n)�������ܼ��l(f��)�W(xu��)�����ҵ���֪�������Ķ�����n��Ч�ʡ�
�����ӑB(t��i)�ֽ�D�Σ�չʾ���}���|(zh��)
������(d��ng)�W(xu��)�����������}�M����̽����������(d��o)�W(xu��)���l(f��)�F(xi��n)���}�ı��|(zh��)���o���ˆ��}3���Ķ����@��̽���^���в��༤�l(f��)�W(xu��)��˼�����������}���R���@���h(hu��n)��(ji��)�ǽ����ή��匢ԭ�D���M�зֽ⣬���N���Ļ����D�ΆΪ�չʾ������ͨ�^�@���ӑB(t��i)չʾ���W(xu��)���l(f��)�F(xi��n)�D�εĽM�Ϻ������^�̣��Mһ���J(r��n)�R�D���P(gu��n)ϵ��
�������}3����ʾ���|(zh��)——�Dz������о����S���Q�ĈD�ζ�������Ƶ���r��?
�����W(xu��)��ͨ�^̽���l(f��)�F(xi��n)�����}�ı��|(zh��)�ǃɂ��S���Q�D�εĽM�φ��}���^�쵽ʹ���}�������cP�����@�ɂ��S���Q�D�εĽ��c����D6��ʾ��
��������(ji��)�nͨ�^�������y���l(f��)�F(xi��n)AH�cPH֮�g�Ĕ�(sh��)���P(gu��n)ϵ��λ���P(gu��n)ϵ�����B(y��ng)�W(xu��)���ĺ�������;�������ή����o���̌W(xu��)���M�����cP��߅BC�����L�����\�ӡ���������׃?y��u)����Ρ����Ρ�ƽ����߅�Σ�̽��߀�Пo��ƵĽY(ji��)Փ?�����ڣ��l��߀������Щ��׃?�Լ����������(d��o)�W(xu��)��˼���Dz������о����S���Q�ĈD�ζ�������Ƶ���r��?�M���@�ӵ��ƏV��ȵ�һϵ��˼�S���B(y��ng)��ʼ�K�B�������һ����о�������
�������Îή������������}�Č��|(zh��)�r������ʹ�W(xu��)������˽�Ҫ��Q���}���P(gu��n)�I���ڡ��c���y(t��ng)�̌W(xu��)����^����������ֱ�^�ط�ӳ���}�����Mһ��������(d��o)�W(xu��)���M�Д�(sh��)�W(xu��)�Č���̽�����ьW(xu��)��(x��)�����ә�(qu��n)�������o�ˌW(xu��)��������{(di��o)���ˌW(xu��)���ČW(xu��)��(x��)�dȤ�������ˌW(xu��)���Ć��}���R�����F(xi��n)�ˌW(xu��)���������x�Ľ���(g��u)��
�������F(xi��n)����Ϣ���g(sh��)�\���ڳ��Д�(sh��)�W(xu��)�̌W(xu��)����Ϣ���r���ı�Ȼڅ�ݣ����Ƅӽ̌W(xu��)�ĸ��߽̌W(xu��)Ч�����Ҫ�ֶΡ�����҂���ҕ�F(xi��n)����Ϣ���g(sh��)���\�ã������n������������M�̌W(xu��)�����\���ڽ̌W(xu��)���`�У�����Փ�о��c���`̽ӑ�Y(ji��)���������@�Ӳ��ܸ�׃������Ч���n�ý̌W(xu��)���ƄӔ�(sh��)�W(xu��)�̌W(xu��)�ĬF(xi��n)�����M�̣����F(xi��n)��Ч�̌W(xu��)��
��������̎����҂���ʲô?�������֪�R�����W(xu��)���z���ˣ����o���ӂ��đ�(y��ng)ԓ��һ�N˼�����}�ķ�����һ�N�о����}�ķ�����һ�N�J(r��n)�R���^������^�c���҂����n֮ǰ���Dz��Ǒ�(y��ng)ԓ�����Լ����Ҟ�ʲôҪ�v�@��(ji��)�n?ͨ�^�@��(ji��)�n��Ҫ�̽o�W(xu��)��ʲô֪�R?��Ҫ�̽o�W(xu��)��ʲô˼�S������?����̎����҂���(y��ng)ԓ˼��ͨ�^�@��(ji��)�n��֪�R�̌W(xu��)���������B(y��ng)�W(xu��)����˼�S���������ή����o���̌W(xu��)ʹԭ���Ďν̌W(xu��)���o�B(t��i)�l(f��)չ��ӑB(t��i)���o�W(xu��)�������ijʬF(xi��n)�ˈD�ε������^�̣����}�ā���ȥ�}���̕��W(xu��)�����˼�����}���������}�������ˌW(xu��)���Ć��}���R��
������Ϣ���g(sh��)��(y��ng)���ڳ��Ў��n�ý̌W(xu��)���c�n�ý̌W(xu��)�ЙC���ںϣ�ʹ��(sh��)�W(xu��)�n�ó�M����͘�Ȥ;������(f��)�s�����֪�R����(sh��)�W(xu��)�n�óɞ�W(xu��)�����W(xu��)�Ę��@����Ϣ���g(sh��)�ڳ��Ўν̌W(xu��)�еđ�(y��ng)�ã��o���n�ý̌W(xu��)������׃�������õ،��F(xi��n)���n�ý̌W(xu��)�F(xi��n)������
�������]��x��������B(y��ng)�W(xu��)���n��(n��i)����������`����
�����@ƪӋ��C���g(sh��)Փ�İl(f��)����������B(y��ng)�W(xu��)���n�Ã�(n��i)����������`������Ӌ��C���A(ch��)�����ڮ�(d��ng)ǰ�W(xu��)У�������ܵ���ҕ��Փ�ĸ���(j��)�Լ��Ĺ�����(j��ng)������ėl;���������W(xu��)����ߌW(xu��)��(x��)�dȤ�ͽ̌W(xu��)Ч����ͨ�^���B(y��ng)�W(xu��)���n���������`���������l(f��)�W(xu��)���ČW(xu��)��(x��)�dȤ����ߌW(xu��)�����ԌW(xu��)������ʹ�����W(xu��)У���F(xi��n)�˔�(sh��)�ֻ��W(w��ng)�j(lu��)��Ϣ�̌W(xu��)��
����