發布時間:2021-12-29所屬分類:電工職稱論文瀏覽:1次
摘 要: 摘要:隨著風電大規模并網,電力系統逐漸發展為低慣量系統,廣泛推廣風電機組轉子慣性控制技術對于提高系統的頻率穩定性具有重要意義。文中通過對雙饋風電機組和火電機組調頻特性的分析以及對雙饋風電機組等效慣性常數的研究,提出了風-火系統模糊自適應虛擬慣量控制策
摘要:隨著風電大規模并網,電力系統逐漸發展為低慣量系統,廣泛推廣風電機組轉子慣性控制技術對于提高系統的頻率穩定性具有重要意義。文中通過對雙饋風電機組和火電機組調頻特性的分析以及對雙饋風電機組等效慣性常數的研究,提出了風-火系統模糊自適應虛擬慣量控制策略。首先根據風電機組運行工況和系統風電滲透率模糊動態決策出了風電場調頻比例系數,其次基于風電機組輔助慣性控制微分系數與風電機組等效慣量常數的關系和風火聯合增量系統模型整定了風電機組虛擬慣性控制參數的變化范圍,最后設計算例驗證了所提自適應調頻控制策略的有效性。仿真結果表明該策略不僅使得風電機組在各種運行工況下均能夠提供可靠的有功支撐,還保證了調頻過程中風電機組的穩定運行,提高了系統的頻率穩定性。
關鍵詞:低慣量系統;雙饋風電機組;等效慣量常數;模糊控制;自適應虛擬慣量
0 引言
近年來,隨著“兩個替代”戰略的推廣實施,系統中風電滲透率不斷提高[1]。然而大規模風電的接入將明顯降低電力系統的抗擾動能力和調頻能力[2-3]。為了削弱含高滲透風電系統的低慣量特性,國內外最新發布的電網導則均要求并網風電機組能夠有參與系統調頻和備用的能力[4]。
目前,國內外學者對風電機組參與調頻的控制策略進行了大量的研究。風電機組的調頻控制,主要通過采用附加控制結構改變自身或儲能模塊的有功輸出來響應系統頻率變化[5]。具體實現方法包括轉子慣性控制[6-8]、功率備用控制[8-9]和綜合協調控制[10-11]以及儲能型虛擬同步機技術[12]等,風電機組均能夠有效的參與系統調頻。其中,風電機組的轉子慣性控制是通過調節風電機組的轉子轉速以釋放出旋轉動能來實現的,其能夠快速地提供慣量支撐以抑制系統頻率惡化,在有效改善系統調頻性能的同時有較好的經濟性[13-14]。為了使風電機組的轉子慣性控制能夠適應電網運行狀態,文獻[15-16] 根據系統頻率變化情況提出了跟蹤系統頻率狀態動態調節慣性控制參數的調頻策略,極大地挖掘了風電的調頻潛力,改善了電網頻率特性。同時,風機轉子中的動能有限,若一味追求風電機組參與系統調頻的能力,系統容易出現頻率的二次跌落事件。基于此,文獻[16-18]依據風機所處環境和自身運行條件提出了變參數控制方法,使得風電機組能夠穩定的參與調頻,避免了系統頻率的二次跌落,改善了系統的頻率響應能力。然而這些控制方法較為繁瑣,難以適應工程應用,且沒有考慮風電機組控制本身的穩定性。
針對風火聯合系統的協調調頻控制,在風火調度層,首先需要解決的是風電場需要分擔的功率缺額比例。文獻[16]以風速分區為基礎,進一步基于模糊邏輯控制方法實現了風電場與儲能系統的靈活配合,實時決定了風電場的短期頻率響應有功增量,提高了系統頻率穩定性;文獻[19]則基于風電機組分區,在確定風電場和火電機組參與調頻的功率參考值的基礎上,進而對風電場調頻功率進行了動態分配。然而,上述文獻均是在風電滲透率不變的場景下所進行的研究,并沒有考慮不同風電滲透率工況下調頻控制方案的適用性。
綜上所述,本文在定位辨析風電、火電調頻特性的基礎上,探究適用于不同風電滲透率工況下的模糊自適應虛擬慣量控制方案。在風火調度層,基于模糊控制根據風電機組運行工況和風電滲透率提出動態決策風電場調頻比例系數的模糊控制策略;在風電機組層,基于風機有效旋轉動能計算得出風電機組的等效慣性常數,分析最大等效慣性常數與轉子轉速的關系,基于慣性控制微分系數與等效慣性常數的關系和風火聯合增量系統模型提出風電機組層模糊虛擬慣量控制方案。仿真結果表示所提策略有效改善了系統的頻率穩定性,提高了系統運行的安全穩定。
1 風電機組虛擬慣量控制
1.1 風火調頻特性辨析
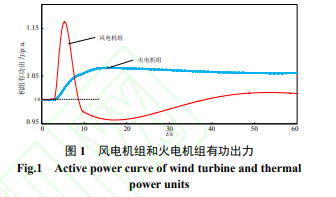
研究含高滲透風電系統的調頻控制,首先要分析、定位風電機組與火電機組參與調頻的調頻特性和調頻任務。目前,雙饋風電機組 (doubly- fed induction generator, DFIG) 是風電場的主流機型,因此本文以 DFIG 作為研究對象,DFIG 參數取值見文獻[6]。此外,為使 DFIG 能夠表現出較穩定的虛擬慣量,本文依據風速變化將 MPPT 運行曲線劃分為如文獻[20]所示的四個區間。考慮到 DFIG 在四個區間的運行特性,本文僅研究運行在 MPPT 區間的 DFIG 及風-火系統的模糊虛擬慣量控制。圖 1 為算例系統發生頻率跌落時風電機組和火電機組的有功出力曲線。
由圖 1 可知,由于風電機組是經電力電子器件并網出力的,對電網表現出較小的慣性時間常數,因此其能夠在頻率擾動的初始迅速提供較大的有功支撐,但持續時間較短,在本系統中僅約為 4s,且在頻率恢復過程中會增加額外的調頻需求,導致當系統中風電出力占比較高時,易出現較嚴重的二次頻降現象[14]。而火電機組具有較大的慣性時間常數,雖然不能快速阻尼系統頻率變化,但其能夠在較長周期的調頻過程中維持穩定的出力,保證了系統頻率的穩定。
綜上所述,在參與系統調頻過程中,應當充分發揮風電場調頻快速性和火電機組調頻持續性的特點,將其分別作為快速、暫態和持久、穩定的有功電源。同時應注意到當系統中風電滲透率較高時,為避免出現嚴重的二次頻降現象,在頻率恢復階段應盡量削弱系統的等效慣性和阻尼作用,以加速系統頻率的恢復。
2 基于 DFIG 有效動能的風-火系統模糊虛擬慣量控制
2.1 DFIG 有效動能
綜合考慮風電機組調頻前后的物理特性,DFIG 有效動能的變化包括兩部分[18],如圖 2 所示,有效動能的變化受機組轉速變化范圍約束。DFIG 有效動能可以用風電機組等效虛擬慣性常數 Hwvir 表示,如式(4)所示,式中變量含義見文獻[18]。
2.2 風-火系統模糊虛擬慣量控制
為了提高風-火系統的調頻性能,本文依據風電場運行條件以及頻率狀態確定了系統的有功增量,實現了風電、火電機組調頻特性的靈活配合。
2.2.1 風火調度層控制策略
為充分利用風電場的調頻容量并適應不同風電滲透率,在風火調度層,利用模糊邏輯控制器 FIS1 確定風電場的調頻比例系數 Kw,具體控制結構如圖 2 所示。對于 FIS1,其輸入量為風電滲透率 w (0.02~1)與風資源條件 (當地的平均風速) Vw(6~10m/s),輸出量為風電場的調頻比例系數 Kw(0~1),其與風電場調頻能力的強弱是正相關的。 FIS1 根據當前系統運行工況下并網風電機組參與調頻的能力來動態確定 Kw,進而決定了系統頻率響應過程中風電場承擔的出力增量,如式(2)所示。
確定 FIS1 的輸入與輸出變量對應關系及隸屬度函數曲線如附錄 A 圖 A2 所示。FIS1 在充分利用風電場調頻潛力的同時避免了對風電場調頻的依賴,保證了系統頻率的穩定性。基于此建立了如表 1 所示的模糊邏輯規則表,該規則表體現了下述的推理原則:當風速 Vw 非常小且風電滲透率 w 較小時,則輸出 Kw要盡可能小;當風速 Vw 較小且風電滲透率 w 較大時,則輸出 Kw 較大;當風速 Vw 較大且風電滲透率 w 較小時,則輸出 Kw 較大;當風速 Vw 較大且風電滲透率 w 較大時,則輸出 Kw 非常大。綜上得到了模糊邏輯系統基于 Mamdani 型的模糊控制輸出結果如圖 4 所示。
2.2.2 機組層控制策略
本節欲建立風電機組層的模糊虛擬慣量控制策略,考慮到風電機組控制參數的實時改變可能對系統整體穩定性產生影響[15,21],針對運行在 MPPT 區間的 DFIG 建立圖 5 所示的風火聯合增量系統模型,以整定控制參數的合理變化范圍,模型中初始化參數取值見附錄 A 表 A1。在額定風速以下 (Vw=9m/s),設定慣性控制參數 Kdf 和 Kpf 均為 1,不斷改變增益系數 Kdfp 和 Kpfp 的取值,進行頻域特征值分析,繪制出影響系統阻尼特性的主導特征根的移動軌跡如圖 6 所示。
對圖 6 進行分析可知,當 Kpfp 較小時,特征根1 會出現正值,由式(3)可知這是因為 Kpfp 的大小與系統阻尼有關,Kpfp 過小會減小系統阻尼,導致系統穩定性不佳,當 Kpfp 增大時特征根1 向左半平面移動,系統穩定性得到改善;當 Kpfp較大時,特征根2 會減小直至移動到右半平面,這是由于 Kpfp 過大會導致風電機組控制本身的失穩。同理分析可知,特征根3 和4 的變化特性同樣會限制 Kdfp 的變化范圍。由此可得,①系數 Kpfp 取值范圍為(- 7~19);②系數 Kdfp 的取值范圍為(-9~11)。因此,將以上取值范圍的子集作為虛擬慣量控制參數的變化范圍能夠保持系統穩定性不受影響。
為達到根據系統頻率波動狀態動態調節系統等效慣量和阻尼且保持風電機組控制穩定性的要求[15,18],本文基于慣性控制系數 Kdf 與等效慣性常數 Hwvir 的關系和風火聯合增量系統模型提出風電機組層模糊虛擬慣量控制,控制結構如圖 7 所示。
如圖 7 所示,在機組控制層,利用風電機組模糊邏輯控制器 FIS2 動態調節慣性控制參數,以改變系統等效慣量和阻尼。對于 FIS2,取系統頻率偏差f ( - 0.005~0 p.u.) 和 頻 率 變 化 率 d dt f ( - 0.012~0.012 p.u./s)[22]為輸入量來有效區分系統頻率波動狀態,輸出量為慣性控制微分系數 Kdf (0~1) 及比例系數 Kpf (-6~6)。FIS2 的輸入與輸出量對應關系及隸屬度函數曲線如附錄 A 圖 A3 所示。
FIS2 根據系統頻率變化實時調整風電機組的有功輸出,動態模擬同步發電機的功頻下垂和慣量響應特性,有效補償了風火系統的等效慣量和阻尼,基于此建立了如表 2 所示的邏輯規則表。
FIS2 體現的推理原則為:當系統頻率偏差f 較小且系統頻率變化率 d dt f 絕對值較小時,則輸出 Kdf要盡可能小,Kpf 為負值且絕對值盡可能大;當系統頻率偏差f 較大且系統頻率變化率 d dt f 為正值時,輸出參數 Kdf 要盡可能小,Kpf 為負值且絕對值盡可能大,使得系統頻率盡快恢復穩定;當系統頻率偏差f 較大且系統頻率變化率 d dt f 為負值時,輸出參數 Kdf 要盡可能大,Kpf為正值且絕對值盡可能大,以減小系統頻率波動。綜上得到了系統基于 Mamdani 型的輸出結果如圖 8 所示。
3 算例分析
為驗證文中所提風-火系統模糊虛擬慣量控制的有效性和風電機組的自適應控制效果,建立附錄 B 圖 B1 所示的兩區域系統模型。區域Ⅰ由 9 臺火電機組構成,單臺機組額定有功為 300MW,其中機組參數按附錄 A 表 A1 取值。區域Ⅱ為風電場,采用單機等值模型,裝機容量為 400MW,風機均運行在 MPPT 區間。負荷消耗的額定功率 PL 為 1600MW,通過設定負荷突增量來模擬頻率跌落事件。本文以保持旋轉備用不變,進行風火容量等比例置換來改變系統的風電占比 w 。仿真驗證項目包括:
1)維持系統風電滲透率不變,將區域Ⅱ中風電機組按風速進行分組,設定發生一定的功率擾動,驗證所提協調調頻策略的可行性,校核風電機組的控制效果。
2)在不同風電滲透率工況下,區域Ⅱ中風電機組的運行風速相同,設定發生同樣的功率擾動,校核系統的調頻性能,驗證所提模糊協調策略的魯棒性。
3.1 同一風電滲透率工況下系統調頻效果分析
設定系統風電滲透率 w 為 25%,根據運行風速,將區域Ⅱ中風電機組按每間隔 1m/s 原則從高到低分為 4 個風速段(R1~R4),每個風速段的機組出力和均為 100MW。仿真 t=2s 時,系統負荷突然增加 22MW,仿真結果如圖 9 所示。
如圖 9(a)所示,當系統發生功率擾動后,風電場參與調頻使得系統頻率最大偏差減小,頻率回復正常值的持續時間增長。對比風電場不參與調頻和風電場以文獻[9, 15]采用的轉子慣性控制進行調頻,本文所提調頻控制策略能夠使系統頻率最快滿足國標要求的±0.2Hz 的頻率波動范圍,系統的頻率響應性能最佳。
圖 9(b)給出了擾動發生后系統中火電、風電機組出力的變化趨勢。由圖可以得出,在本文所提調頻控制策略下,風電機組能夠快速地增發有功輸出,補償了火電機組有功支撐的延時性;此外,結合圖 9(a)分析可知,風電機組轉速恢復時的額外有功需求降低了系統頻率的回復速度,這說明風電機組輔助調頻是以延長頻率回復時間為代價的。
圖 9(c)給出 FIS2 前 40s 的仿真結果。由圖可知,在不同頻率變化階段,風電機組模糊慣性控制參數是不斷變化的。結合圖 9(a)分析,在頻率兩次下降期間,控制參數 Kdf 和 Kpf的快速增加有效阻尼了系統頻率的惡化和加速了系統頻率的恢復。此外,輸出控制參數曲線具有幅值小且持續時間短的沖擊型脈動,分析表明該類脈動是可忽略的。
針對本文所提協調調頻控制策略,由于區域Ⅱ 中風電機組所處風速段不同,因此在頻率支撐期間每個風速段風電機組的有功出力和轉速變化情況也有所不同,具體變化情況如圖 10 所示。
對圖 10 分析可知,每個風速段的風電機組在頻率波動期間均能夠提供功率支撐,并且隨著風速段等級的提高,風電機組短時有功值逐漸增大,最大為 1.036p.u.;有功支撐(有功出力在 1.0p.u.以上) 時間也逐漸增加,最長為 5.9s,即風電機組短時釋放的動能逐漸增多;同時風電機組的轉速變化幅度也逐漸增大,最大為 0.003p.u.。
進一步對圖 9(a)和圖 10(b)進行分析,風電機組轉速恢復的同時,系統頻率曲線有下凹趨勢,但很快又重新恢復,這是因為機組層控制策略以 2Hwmax 作為慣性控制微分系數 Kdf 的最大取值,在提高系統等效慣量的同時又避免了對風電機組的過度依賴,保證了機組的運行穩定;同時可以得出由于不同風速段的風電機組表現出的最大慣量是不同的,因此風電機組是依次進入轉速恢復階段的,在一定程度上削弱了二次頻降的強度。——論文作者:盛四清,李朋旺,張立偉,樊茂森
SCISSCIAHCI